使用Actor-Critic的DDPG强化学习算法控制双关节机械臂

在本文中，我们将介绍在 Reacher 环境中训练智能代理控制双关节机械臂，这是一种使用 Unity ML-Agents 工具包开发的基于 Unity 的模拟程序。 我们的目标是高精度的到达目标位置，所以这里我们可以使用专为连续状态和动作空间设计的最先进的Deep Deterministic Policy Gradient (DDPG) 算法。

现实世界的应用程序
机械臂在制造业、生产设施、空间探索和搜救行动中发挥着关键作用。控制机械臂的高精度和灵活性是非常重要的。通过采用强化学习技术，可以使这些机器人系统实时学习和调整其行为，从而提高性能和灵活性。强化学习的进步不仅有助于我们对人工智能的理解，而且有可能彻底改变行业并对社会产生有意义的影响。

而Reacher是一种机械臂模拟器，常用于控制算法的开发和测试。它提供了一个虚拟环境，模拟了机械臂的物理特性和运动规律，使得开发者可以在不需要实际硬件的情况下进行控制算法的研究和实验。

Reacher的环境主要由以下几个部分组成：

机械臂：Reacher模拟了一个双关节机械臂，包括一个固定基座和两个可动关节。开发者可以通过控制机械臂的两个关节来改变机械臂的姿态和位置。
目标点：在机械臂的运动范围内，Reacher提供了一个目标点，目标点的位置是随机生成的。开发者的任务是控制机械臂，使得机械臂的末端能够接触到目标点。
物理引擎：Reacher使用物理引擎来模拟机械臂的物理特性和运动规律。开发者可以通过调整物理引擎的参数来模拟不同的物理环境。
视觉界面：Reacher提供了一个可视化的界面，可以显示机械臂和目标点的位置，以及机械臂的姿态和运动轨迹。开发者可以通过视觉界面来调试和优化控制算法。
Reacher模拟器是一个非常实用的工具，可以帮助开发者在不需要实际硬件的情况下，快速测试和优化控制算法。

模拟环境

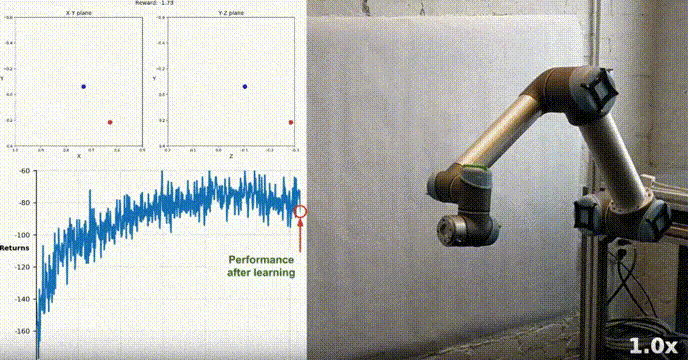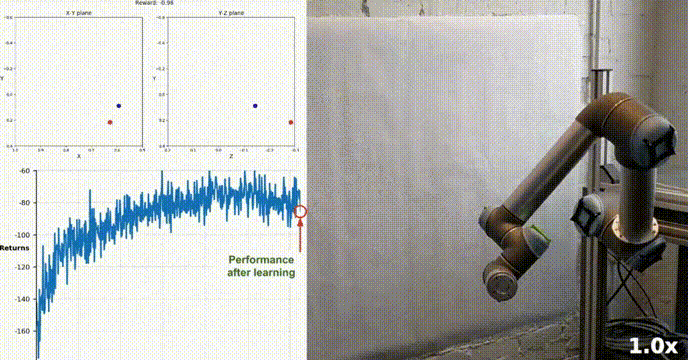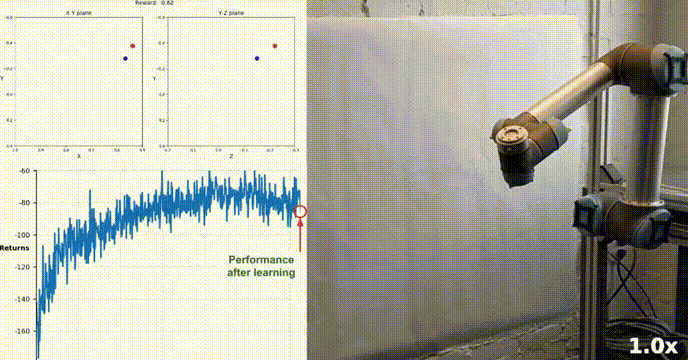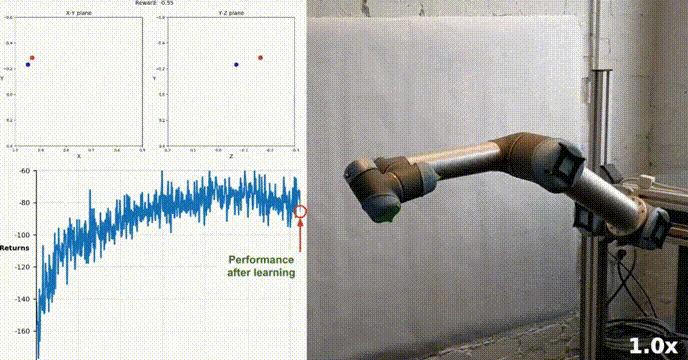
Reacher 使用 Unity ML-Agents 工具包构建，我们的代理可以控制双关节机械臂。 目标是引导手臂朝向目标位置并尽可能长时间地保持其在目标区域内的位置。 该环境具有 20 个同步代理，每个代理独立运行，这有助于在训练期间有效地收集经验。

状态和动作空间

了解状态和动作空间对于设计有效的强化学习算法至关重要。 在 Reacher 环境中，状态空间由 33 个连续变量组成，这些变量提供有关机械臂的信息，例如其位置、旋转、速度和角速度。 动作空间也是连续的，四个变量对应于施加在机械臂两个关节上的扭矩。 每个动作变量都是一个介于 -1 和 1 之间的实数。

任务类型和成功标准

Reacher 任务被认为是片段式的，每个片段都包含固定数量的时间步长。 代理的目标是在这些步骤中最大化其总奖励。 手臂末端执行器保持在目标位置的每一步都会获得 +0.1 的奖励。 当代理在连续 100 次操作中的平均得分达到 30 分或以上时，就认为成功。

了解了环境，下面我们将探讨 DDPG 算法、它的实现，以及它如何有效地解决这种环境中的连续控制问题。

连续控制的算法选择：DDPG
当涉及到像Reacher问题这样的连续控制任务时，算法的选择对于实现最佳性能至关重要。在这个项目中，我们选择了DDPG算法，因为这是一种专门设计用于处理连续状态和动作空间的actor-critic方法。

DDPG算法通过结合两个神经网络，结合了基于策略和基于值的方法的优势:行动者网络(Actor network)决定给定当前状态下的最佳行为，批评家网络(Critic network)估计状态-行为值函数(Q-function)。这两种网络都有目标网络，通过在更新过程中提供一个固定的目标来稳定学习过程。

通过使用Critic网络估计q函数，使用Actor网络确定最优行为，DDPG算法有效地融合了策略梯度方法和DQN的优点。这种混合方法允许代理在连续控制环境中有效地学习。

import random
from collections import deque
import torch
import torch.nn as nn
import numpy as np

from actor_critic import Actor, Critic

class ReplayBuffer:
def __init__(self, buffer_size, batch_size):
self.memory = deque(maxlen=buffer_size)
self.batch_size = batch_size

def add(self, state, action, reward, next_state, done):
self.memory.append((state, action, reward, next_state, done))

def sample(self):
batch = random.sample(self.memory, self.batch_size)
states, actions, rewards, next_states, dones = zip(*batch)
return states, actions, rewards, next_states, dones

def __len__(self):
return len(self.memory)


class DDPG:
def __init__(self, state_dim, action_dim, hidden_dim, buffer_size, batch_size, actor_lr, critic_lr, tau, gamma):
self.actor = Actor(state_dim, hidden_dim, action_dim, actor_lr)
self.actor_target = Actor(state_dim, hidden_dim, action_dim, actor_lr)
self.critic = Critic(state_dim, action_dim, hidden_dim, critic_lr)
self.critic_target = Critic(state_dim, action_dim, hidden_dim, critic_lr)

self.memory = ReplayBuffer(buffer_size, batch_size)
self.batch_size = batch_size
self.tau = tau
self.gamma = gamma

self._update_target_networks(tau=1) # initialize target networks

def act(self, state, noise=0.0):
state = torch.tensor(state, dtype=torch.float32).unsqueeze(0)
action = self.actor(state).detach().numpy()[0]
return np.clip(action + noise, -1, 1)

def store_transition(self, state, action, reward, next_state, done):
self.memory.add(state, action, reward, next_state, done)

def learn(self):
if len(self.memory) < self.batch_size:
return

states, actions, rewards, next_states, dones = self.memory.sample()

states = torch.tensor(states, dtype=torch.float32)
actions = torch.tensor(actions, dtype=torch.float32)
rewards = torch.tensor(rewards, dtype=torch.float32).unsqueeze(1)
next_states = torch.tensor(next_states, dtype=torch.float32)
dones = torch.tensor(dones, dtype=torch.float32).unsqueeze(1)

# Update Critic
self.critic.optimizer.zero_grad()

with torch.no_grad():
next_actions = self.actor_target(next_states)
target_q_values = self.critic_target(next_states, next_actions)
target_q_values = rewards + (1 - dones) * self.gamma * target_q_values

current_q_values = self.critic(states, actions)
critic_loss = nn.MSELoss()(current_q_values, target_q_values)

critic_loss.backward()
self.critic.optimizer.step()

# Update Actor
self.actor.optimizer.zero_grad()

actor_loss = -self.critic(states, self.actor(states)).mean()
actor_loss.backward()
self.actor.optimizer.step()

# Update target networks
self._update_target_networks()

def _update_target_networks(self, tau=None):
if tau is None:
tau = self.tau

for target_param, param in zip(self.actor_target.parameters(), self.actor.parameters()):
target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)

for target_param, param in zip(self.critic_target.parameters(), self.critic.parameters()):
target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)

上面的代码还使用了Replay Buffer，这可以提高学习效率和稳定性。Replay Buffer本质上是一种存储固定数量的过去经验或过渡的内存数据结构，由状态、动作、奖励、下一状态和完成信息组成。使用它的主要优点是使代理能够打破连续经验之间的相关性，从而减少有害的时间相关性的影响。

通过从缓冲区中抽取随机的小批量经验，代理可以从一组不同的转换中学习，这有助于稳定和概括学习过程。 Replay Buffer还可以让代理多次重用过去的经验，从而提高数据效率并促进从与环境的有限交互中更有效地学习。

DDPG算法是一个很好的选择，因为它能够有效地处理连续的动作空间，这是这个环境的一个关键方面。该算法的设计允许有效地利用多个代理收集的并行经验，从而实现更快的学习和更好的收敛。就像上面介绍的Reacher 可以同时运行20个代理，所以我们可以使用这20个代理进行分享经验，集体学习，提高学习速度。

完成了算法，下面我们将介绍、超参数选择和训练过程。

DDPG算法在Reacher 环境中工作
为了更好地理解算法在环境中的有效性，我们需要仔细研究学习过程中涉及的关键组件和步骤。

网络架构

DDPG算法采用两个神经网络，Actor 和Critic。两个网络都包含两个隐藏层，每个隐藏层包含400个节点。隐藏层使用ReLU (Rectified Linear Unit)激活函数，而Actor网络的输出层使用tanh激活函数产生范围为-1到1的动作。Critic网络的输出层没有激活函数，因为它直接估计q函数。

以下是网络的代码:

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim

class Actor(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim, learning_rate=1e-4):
super(Actor, self).__init__()

self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, hidden_dim)
self.fc3 = nn.Linear(hidden_dim, output_dim)

self.tanh = nn.Tanh()

self.optimizer = optim.Adam(self.parameters(), lr=learning_rate)

def forward(self, state):
x = torch.relu(self.fc1(state))
x = torch.relu(self.fc2(x))
x = self.tanh(self.fc3(x))
return x

class Critic(nn.Module):
def __init__(self, state_dim, action_dim, hidden_dim, learning_rate=1e-4):
super(Critic, self).__init__()

self.fc1 = nn.Linear(state_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim + action_dim, hidden_dim)
self.fc3 = nn.Linear(hidden_dim, 1)

self.optimizer = optim.Adam(self.parameters(), lr=learning_rate)

def forward(self, state, action):
x = torch.relu(self.fc1(state))
x = torch.relu(self.fc2(torch.cat([x, action], dim=1)))
x = self.fc3(x)
return x

超参数选择

选择的超参数对于高效学习至关重要。在这个项目中，我们的Replay Buffer大小为200,000，批大小为256。演员Actor的学习率为5e-4，Critic的学习率为1e-3，soft update参数(tau)为5e-3，gamma为0.995。最后还加入了动作噪声，初始噪声标度为0.5，噪声衰减率为0.998。

训练过程

训练过程涉及两个网络之间的持续交互，并且20个平行代理共享相同的网络，模型会从所有代理收集的经验中集体学习。这种设置加快了学习过程，提高了效率。

from collections import deque
import numpy as np
import torch

from ddpg import DDPG

def train_ddpg(env, agent, episodes, max_steps, num_agents, noise_scale=0.1, noise_decay=0.99):
scores_window = deque(maxlen=100)
scores = []

for episode in range(1, episodes + 1):
env_info = env.reset(train_mode=True)[brain_name]
states = env_info.vector_observations
agent_scores = np.zeros(num_agents)

for step in range(max_steps):
actions = agent.act(states, noise_scale)
env_info = env.step(actions)[brain_name]
next_states = env_info.vector_observations
rewards = env_info.rewards
dones = env_info.local_done

for i in range(num_agents):
agent.store_transition(states[i], actions[i], rewards[i], next_states[i], dones[i])
agent.learn()

states = next_states
agent_scores += rewards
noise_scale *= noise_decay

if np.any(dones):
break

avg_score = np.mean(agent_scores)
scores_window.append(avg_score)
scores.append(avg_score)

if episode % 10 == 0:
print(f"Episode: {episode}, Score: {avg_score:.2f}, Avg Score: {np.mean(scores_window):.2f}")

# Saving trained Networks
torch.save(agent.actor.state_dict(), "actor_final.pth")
torch.save(agent.critic.state_dict(), "critic_final.pth")

return scores

if __name__ == "__main__":
env = UnityEnvironment(file_name='Reacher_20.app')
brain_name = env.brain_names[0]
brain = env.brains[brain_name]

state_dim = 33
action_dim = brain.vector_action_space_size

num_agents = 20

# Hyperparameter suggestions
hidden_dim = 400
batch_size = 256
actor_lr = 5e-4
critic_lr = 1e-3
tau = 5e-3
gamma = 0.995
noise_scale = 0.5
noise_decay = 0.998

agent = DDPG(state_dim, action_dim, hidden_dim=hidden_dim, buffer_size=200000, batch_size=batch_size,
actor_lr=actor_lr, critic_lr=critic_lr, tau=tau, gamma=gamma)

episodes = 200
max_steps = 1000

scores = train_ddpg(env, agent, episodes, max_steps, num_agents, noise_scale=0.2, noise_decay=0.995)

训练过程中的关键步骤如下所示：

初始化网络：代理使用随机权重初始化共享的 Actor 和 Critic 网络及其各自的目标网络。 目标网络在更新期间提供稳定的学习目标。

与环境交互：每个代理使用共享的 Actor 网络，通过根据其当前状态选择动作来与环境交互。 为了鼓励探索，在训练的初始阶段还将噪声项添加到动作中。 采取行动后，每个代理都会观察由此产生的奖励和下一个状态。
存储经验：每个代理将观察到的经验（状态、动作、奖励、next_state）存储在共享重放缓冲区中。 该缓冲区包含固定数量的近期经验，这样每个代理能够从所有代理收集的各种转换中学习。
从经验中学习：定期从共享重放缓冲区中抽取一批经验。 通过最小化预测 Q 值和目标 Q 值之间的均方误差，使用采样经验来更新共享 Critic 网络。
更新 Actor 网络：共享 Actor 网络使用策略梯度进行更新，策略梯度是通过采用共享 Critic 网络关于所选动作的输出梯度来计算的。 共享 Actor 网络学习选择最大化预期 Q 值的动作。
更新目标网络：共享的 Actor 和 Critic 目标网络使用当前和目标网络权重的混合进行软更新。 这确保了稳定的学习过程。
结果展示
我们的agent使用DDPG算法成功地学会了在Racher环境下控制双关节机械臂。在整个训练过程中，我们根据所有20个代理的平均得分来监控代理的表现。随着智能体探索环境和收集经验，其预测奖励最大化最佳行为的能力显著提高。

可以看到代理在任务中表现出了显著的熟练程度，平均得分超过了解决环境所需的阈值(30+)，虽然代理的表现在整个训练过程中有所不同，但总体趋势呈上升趋势，表明学习过程是成功的。

该图显示了20个代理的平均得分:

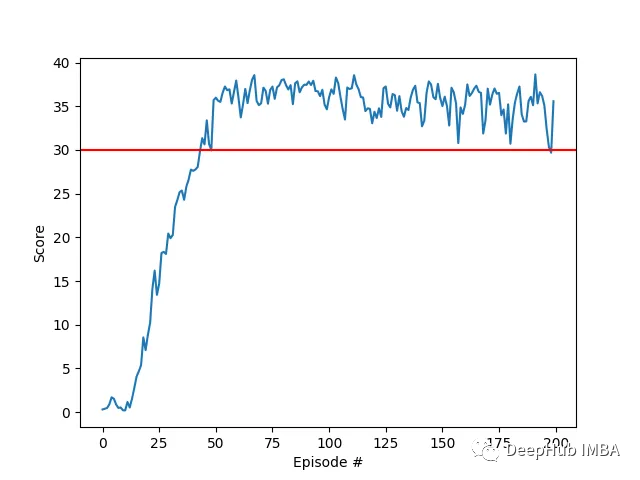
可以看到我们实现的DDPG算法，有效地解决了Racher环境的问题。代理能够调整自己的行为，并在任务中达到预期的性能。

下一步工作
本项目中的超参数是根据文献和实证测试的建议组合选择的。还可以通过系统超参数调优的进一步优化可能会带来更好的性能。

多agent并行训练:在这个项目中，我们使用20个agent同时收集经验。使用更多代理对整个学习过程的影响可能会导致更快的收敛或提高性能。

批归一化:为了进一步增强学习过程，在神经网络架构中实现批归一化是值得探索的。通过在训练过程中对每一层的输入特征进行归一化，批归一化可以帮助减少内部协变量移位，加速学习，并潜在地提高泛化。将批处理归一化加入到Actor和Critic网络可能会导致更稳定和有效的训练，但是这个需要进一步测试。

本文完整代码：

https://avoid.overfit.cn/post/54829204a5c74f0bb2b3a686c5fe079f

引用：

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D., & Wierstra, D. (2015). Continuous control with deep reinforcement learning.
Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., … & Hassabis, D. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529–533.
Udacity Deep Reinforcement Learning Nanodegree.
Barth-Maron, G., Hoffman, M. W., Budden, D., Dabney, W., Horgan, D., TB, D., & Lillicrap, T. (2018). Distributed Distributional Deterministic Policy Gradients. arXiv preprint arXiv:1804.08617.

作者：Gabriel Cassimiro

————————————————

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/deephub/article/details/130594848