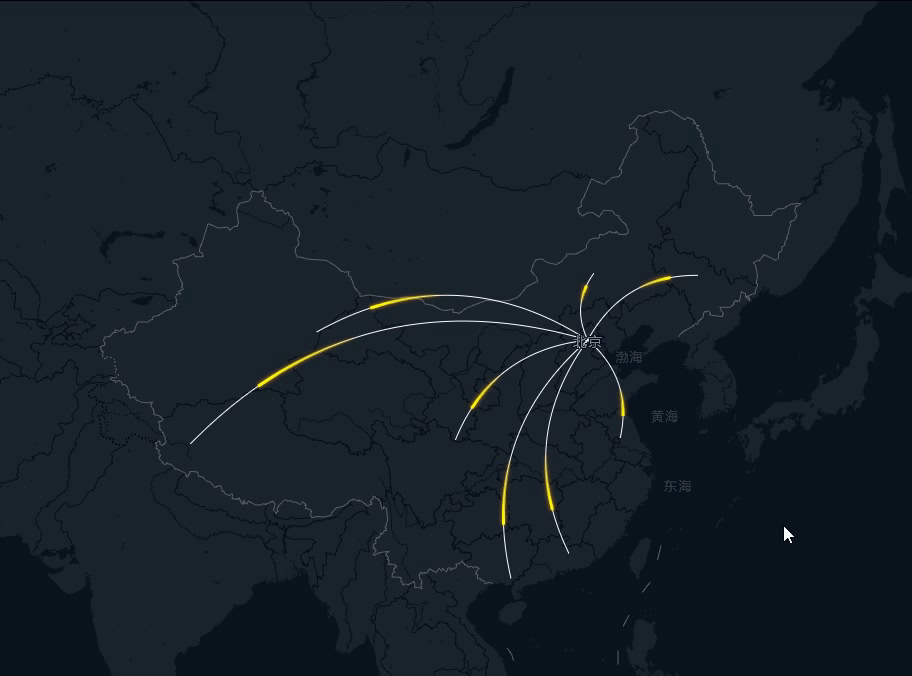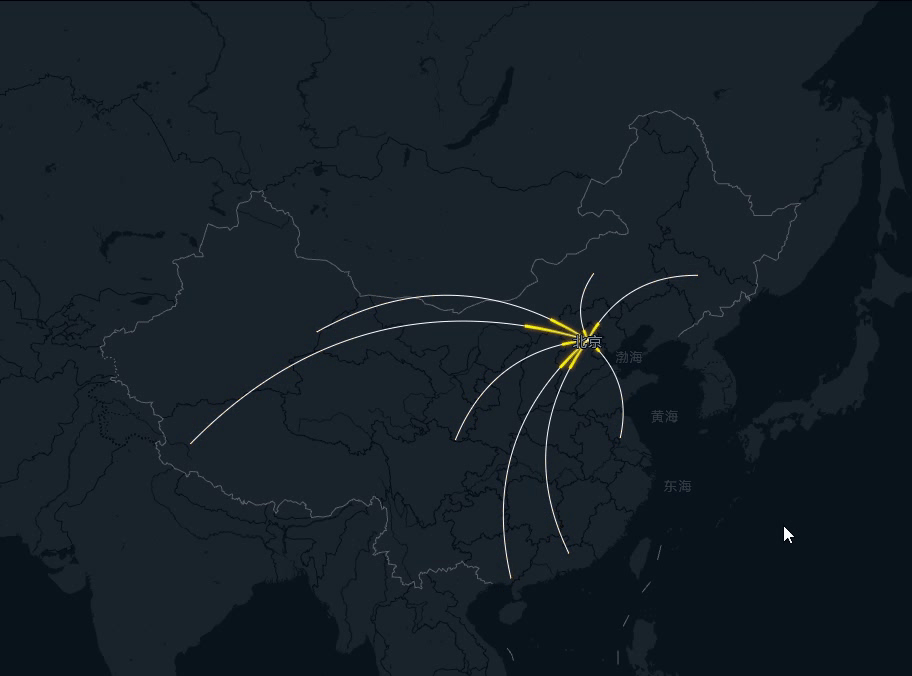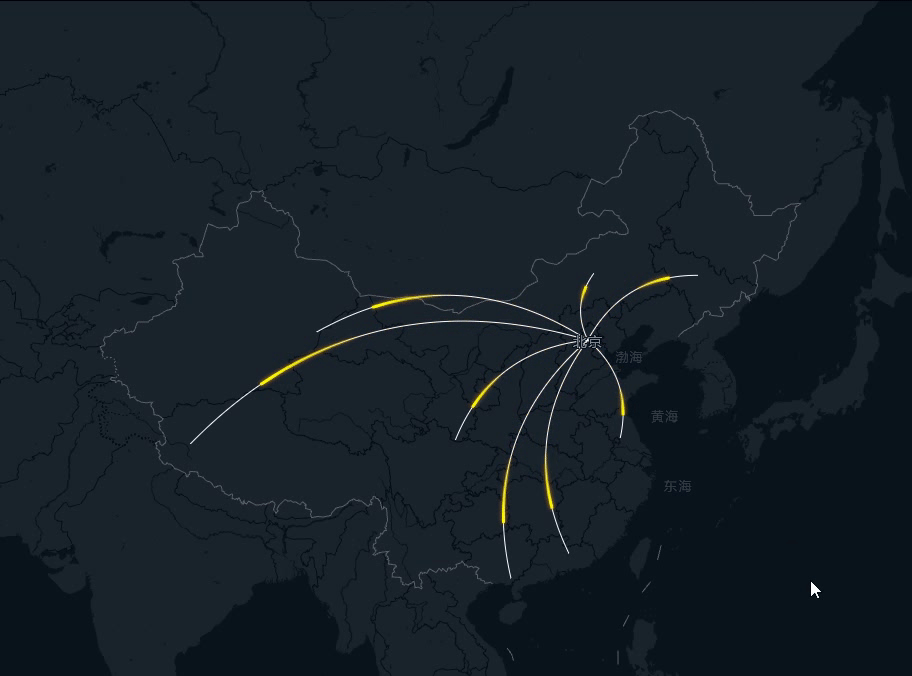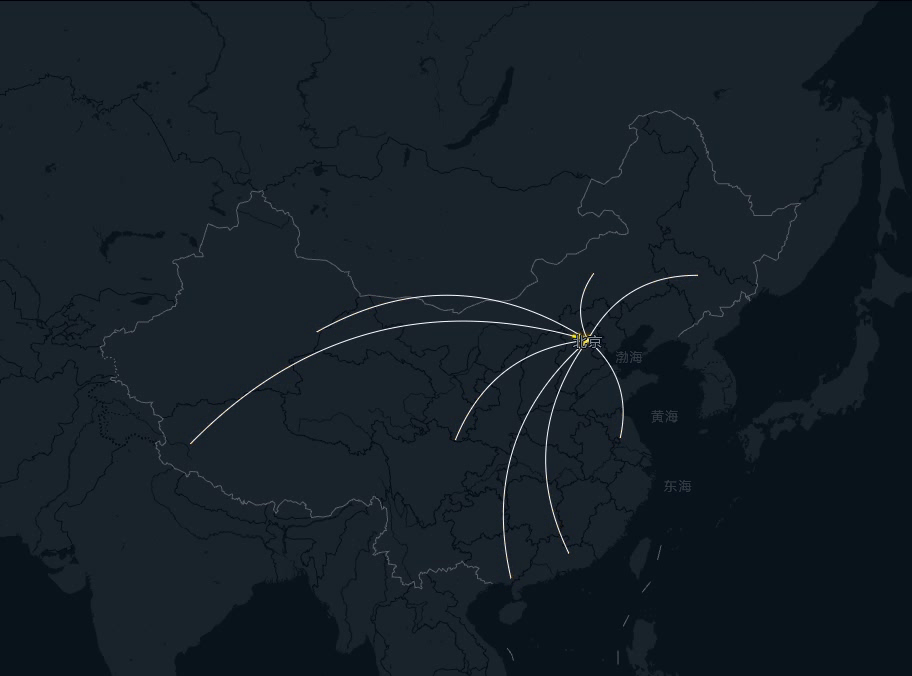
飞线是地图类组件常用的一种效果,往往由一条底线和一条不断移动的曲线构成,当然底线也是可以去掉的,这里展示底线是为了让大家更直观得看到飞线的完整轨迹。
1.canvas相关api。此处由衷感谢MDN和firefox,MDN现在内置了AI Help功能,用chat-gpt3.5协助开发者找资料,贼方便。
a.quadraticCurveTo,绘制二次贝塞尔曲线的函数,调用方法:ctx.quadraticCurveTo(x1,y1,x2,y2),x1,y1是控制点的坐标,x2,y2是终点坐标。
b.setLineDash,定义线条虚线样式的函数,调用方法:ctx.setLineDash([10,100]),传入一个数组,数组元素是数值,用于决定线条的实线和虚线部分长度,传入空数组即为全实线。
c.lineDashOffset,用于调设置虚线的偏移值,调用方法:ctx.lineDashOffset = 100,完成飞线动画的过程其实就是不断修改这个值的过程。类似于svg中的 stroke-dasharray 和 stroke-dashoffset。
d.createLinearGradient,用于创建一个渐变色对象,调用方法:
//渐变色将从(x1,y1)变化至(x2,y2),其余部分将会是纯色。
//在飞线动画中,我们需要再每一帧,根据二次贝塞尔公式,计算出飞线的‘头’和‘尾’,来决定渐变的起始点和终点
let gradient = ctx.createLinearGradient(x1,y1,x2,y2);
gradient.addColorStop(0,"red"); //添加渐变色
gradient.addColorStop(1,"blue");
ctx.strokeStyle = gradient; //将渐变色赋予画布描边色2.三角函数相关知识,sin,cos,tan,asin,acos,atan。
3.二次贝塞尔公式,B (t)= (1-t)^2*P0+2t (1-t)P1+t^2*P2,t∈ [0,1]。
1.首先准备飞线数据如下:
[
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 965.8583040000003,
"y": 474.319496095487
}
},
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 827.2892928000001,
"y": 641.2091882491195
}
},
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 883.002333866667,
"y": 779.4123862210777
}
},
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 940.9379669333339,
"y": 754.4501021810111
}
},
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 562.3410687999999,
"y": 644.9136097572509
}
},
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 688.7202702222226,
"y": 532.9837587351926
}
},
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 992.1560803555558,
"y": 639.1862874174531
}
},
{
"start": {
"x": 959.7895907555558,
"y": 541.0753750091362
},
"end": {
"x": 1070.0379363555558,
"y": 476.342401524088
}
}
]2.飞线数据只提供了起始点(p0)和终点坐标(p1),为了绘制贝塞尔曲线,我们需要第三个点作为控制点。为了确定第三个点(p2)的位置,我们需要引入一个变量来控制曲线的弯曲程度,这里我们暂时称这个变量为曲率(curveness),曲率范围是[0,1]。那么我们怎么根据曲率来确定第三个点呢?首先我们需要计算出p0p1这条线段的中点(pc),弧度(rad)以及长度(distance),在pc上作垂线,根据curveness*distance得到高(h),这样curveness越大,h就越大,且h的值不会超过distance,导致飞线过于弯曲而影响美观。最后根据 h和rad 的值,结合三角函数就能计算出p2的坐标点了。示意图如下,其中的 rad 未标识,其实就是 90°-∠p1pcB 的弧度值:
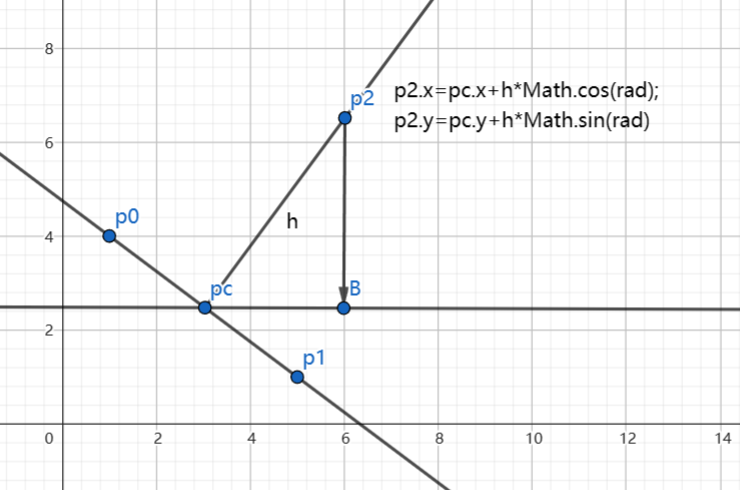
计算中间点的算法:
//p1是起点,p2是终点,radius是曲率curveness,自己决定值,[0,1]范围内即可。
export const calcQuadraticCenterPoint=(p1, p2, radius)=>{
const { x:x1, y:y1 } = p1, { x:x2, y:y2 } = p2;
const deltaX = x2-x1, deltaY = y2-y1;
const height = radius*Math.sqrt(deltaX**2+deltaY**2);
//如果线段垂直于x轴,就可以直接得到中间点的结果了。
if(!deltaX){
return {
x:x1-height,
y:y1+deltaY/2
}
}
const centerX = x1+deltaX/2, centerY = y1+deltaY/2;
//由于canvas的y轴是向下的,我们又希望飞线是向上弯曲的,所以这里的弧度计算需要 -Math.PI/2
let rad = Math.atan(deltaY/deltaX)-Math.PI/2;
return {
x:centerX+Math.cos(rad)*height,
y:centerY+Math.sin(rad)*height
}
}3.得到控制点后,我们就可以绘制飞线的底线了,虽然底线是静止的,但是考虑到我们后续还要绘制飞线动画,这里我们就直接用一个requestAnimationFrame开启每帧绘制了。
this.timer=null; //动画计时器
//封装绘制飞线的二次贝塞尔曲线
const drawFlyLine = (start, end, center)=>{
const ctx = this.ctx; //this.ctx是canvas的上下文
ctx.beginPath();
ctx.moveTo( start.x, start.y );
ctx.quadraticCurveTo( center.x, center.y, end.x, end.y );
ctx.stroke();
ctx.closePath();
}
//绘制函数的入口
const draw=()=>{
const ctx = this.ctx;
const animation = ()=>{
ctx.clearRect(0,0,width, height); //canvas的宽高自行获取
this.flyLineData.forEach((d,i)=>{ //this.flyLineData就是得到控制点后的点位数据
const { start, center, end } = d;
ctx.save();
// 绘制底线
if(showBase){
ctx.lineWidth=2;
ctx.strokeStyle="white";
drawFlyLine(start,end,center);
}
ctx.restore();
});
this.timer = requestAnimationFrame(animation);
}
animation();
}
draw();4.接下来我们绘制飞线,在准备工作中,我们有提到 lineDashOffset 这个api,在每一帧的动画中,我们修改 lineDashOffset的值,就能做到让飞线动起来的效果。不过在绘制飞线前,我们还需以确定以下几个变量的值:
a.飞线长度(length),范围在[0,1]之间。
b.飞线轨迹长度(lineLength),计算贝塞尔曲线长度的算法网上有,这里用最简单的分段法来计算。
二次贝塞尔曲线长度算法:
export const distance = (p0,p1)=>{
const dx = p1.x-p0.x, dy = p1.y-p0.y;
return Math.sqrt(dx**2+dy**2);
}
export const quadraticBezier=(start, end, center, t)=>{
const x = Math.pow(1 - t, 2) * start.x + 2 * (1 - t) * t * center.x + Math.pow(t, 2) * end.x;
const y = Math.pow(1 - t, 2) * start.y + 2 * (1 - t) * t * center.y + Math.pow(t, 2) * end.y;
return {x,y};
}
export const calcQuadraticLength=(start,center,end)=>{
let steps = 100; //这里将曲线划分成了100段去计算长度,为了提高精度也可以增加段数
let length=0;
for(let i=0;i<steps;i++){
const p0 = quadraticBezier(start, end, center, i/steps);
const p1 = quadraticBezier(start, end, center, (i+1)/steps);
length+=distance(p0,p1);
}
return length;
}c.动画步长(step),范围也在[0,1+length]之间,用于表示飞线飞行进度,为什么右区间是 1+length呢?当然是为了让飞线能够完全消失啦。否则第一段飞线还没飞完,第二段就要出来了。
下面是完整的飞线动画绘制方法:
this.timer=null; //动画计时器
//封装绘制飞线的二次贝塞尔曲线
const drawFlyLine = (start, end, center)=>{
const ctx = this.ctx; //this.ctx是canvas的上下文
ctx.beginPath();
ctx.moveTo( start.x, start.y );
ctx.quadraticCurveTo( center.x, center.y, end.x, end.y );
ctx.stroke();
ctx.closePath();
}
draw=()=>{
const ctx = this.ctx;
let length = 0.4;
let step = 0; //动画步长
let width = this.canvas.width;
let height = this.canvas.height;
//粗略获取贝塞尔曲线长度,用于设置dashoffset
let curvesLength = this.flyLineData.map(d=>{
return calcQuadraticLength(d.start, d.center, d.end);
});
const animation = ()=>{
ctx.clearRect(0,0,width, height);
this.flyLineData.forEach((d,i)=>{
const { start, center, end } = d;
const lineLength = curvesLength[i];
ctx.save();
// 绘制底线
if(showBase){
ctx.lineWidth=2;
ctx.strokeStyle='red';
this.drawFlyLine(start,end,center);
}
//绘制飞线
ctx.lineWidth = 3;
ctx.setLineDash([length*lineLength, lineLength]);
ctx.lineDashOffset = -(1+step)*lineLength;
//每一帧计算飞线的头和尾坐标,根据头尾坐标来决定渐变方向
const p1 = quadraticBezier(start, end, center, Math.min(1,step));
const p2 = quadraticBezier(start, end, center, Math.max(0,step-length));
const gradient = ctx.createLinearGradient(p1.x,p1.y,p2.x,p2.y);
//linear.stops是一个对象数组,对象结构如下:{offset:100,color:"#f0f"}
linear.stops.forEach(v=>{
gradient.addColorStop(v.offset/100,v.color);
});
ctx.strokeStyle = gradient;
this.drawFlyLine(start,end,center);
ctx.restore();
});
//step每一帧增加0.01/3,并且利用取余数的方法,在达到1+length时进行重置
step=(((step+0.01/3)*100)%(100*(1+length)))/100;
this.timer = requestAnimationFrame(animation);
}
//在头部图片资源加载完毕后再执行动画
animation();
}
draw(); 至此,一个简单的二次贝塞尔飞线就完成了。
利用setLineDash和lineDashOffset其实可以完成大部分的流光动画,再结合分段算法计算出轨迹的大致长度,我们就可以精准的控制流光的运动。当然,如果你不需要控制流光的数量和位置,不计算轨迹长度也可。
文章
3.45K人气
8粉丝
1关注
 扫一扫关注公众号
扫一扫关注公众号
 扫一扫联系客服
扫一扫联系客服
©Copyrights 2016-2022 杭州易知微科技有限公司 浙ICP备2021017017号-3  浙公网安备33011002011932号
浙公网安备33011002011932号
互联网信息服务业务 合字B2-20220090
